#50 Section6 分類(3)モデルの評価・比較
ここからは、『compare_models』関数を体験していきます。
PyCaretでは『compare_models』関数により、ライブラリで使用可能なすべてのアルゴリズム(『モデル』と言います)を交差検証を用いて訓練し、評価指標を算出して性能を評価します。
既に、『setup』で交差検証は、StratifiedKFold(K分割交差検証)と指定しています(デフォルトですが…)ので、関数型API、もしくはオブジェクト指向APIのどちらかの流儀で、下記のようにコードを書くことにより、様々なアルゴリズムの性能評価を比較できます。
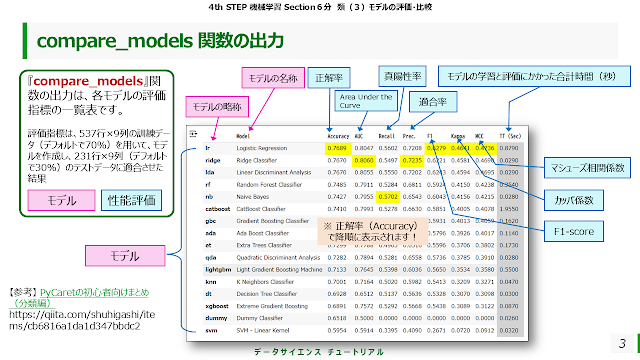
この『compare_models』関数は、537行×9列の訓練データ(デフォルトで70%)を用いて、モデルを作成し、231行×9列(デフォルトで30%)のテストデータに適合させた結果の評価指標を算出します。
具体的には、下図のようになります。
左側の列から『モデルの略称』、『モデルの名称』が『正解率(Accuracy)』で降順に表示されています。正解率より右側の列は、それぞれ性能を表す評価指標となっています。
もっと詳しく知りたい方は、下記の『PyCaretの初心者向けまとめ(分類編)』を参照ください。
次に、性能評価の元になる混同行列を説明します。
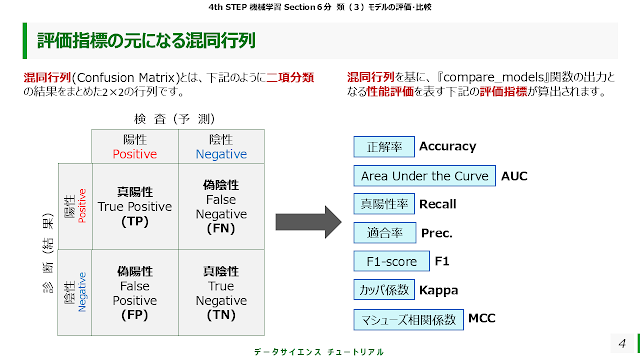
下図の左側の表のように、二項分類の結果をまとめた2×2の行列を混同行列(Confusion Matrix)といいます。
横軸に予測、縦軸に結果のそれぞれの二値(二項)、すなわち陽性or陰性の個数が算出された2×2の行列となっています。臨床の現場では、予測を検査結果、結果を診断と表現するとわかりやすいと思います。この混同行列をもとにさらに算出されるのが、性能評価を表す右側の評価指標です。
それぞれを詳しく見ていきましょう。まずは、
① 正解率(Accuracy)
正解率は、予測結果が実際に当たっていた割合を表します。
具体的に説明すると、ピンクの部分の和、すなわち、検査で陽性かつ診断でも陽性(TP)と検査で陰性かつ診断でも陰性(TN)の和を分子に、分母に全体の和を算出した比率のことです。
② AUC(Area Under the Curve)
AUCとは、主に二値分類問題に対する評価指標の一つで、「ROC曲線の下の面積」を意味します。
ちなみに、下図のグラフは、横軸を混同行列の「偽陽性率(FP率)」、縦軸を「真陽性率(TP率)」にして、数値をプロットしたもので、ROC曲線と呼ばれます。ROC曲線が、対角線より左上にあればあるほど予測性能が高いということができます。
また、グラフの右下に書かれている赤枠で囲んだところは、それぞれのAUCが書かれています。
それを見ると、クラス「0」とクラス「1」それぞれのROC曲線は、AUCが0.86であり、両クラスに対して同程度の性能を示していることがわかります。マイクロ平均とマクロ平均は、
二項分類にはあまり関係がありませんので、説明は割愛します。各データを3以上のカテゴリーに分類する場合(多項分類)のAUCの算出方法の違いによるものだと思っておいてください。詳しくは、下記を参照ください。
【参考】 マイクロ平均とマクロ平均
この指標は、0.0(=0%)~1.0(=100%)の範囲の値を取り、1.0に近いほどモデルの予測性能が高いことを示します。
ACUに関しては、おおまかに下記のような判断をします。
0.9~1.0: 非常によい(excellent)
0.8~0.9: よい(good)
0.7~0.8: まあまあ(fair)
0.6~0.7: よくない(poor)
0.5~0.6: 失敗(fail)
【出典】 AUC(Area Under the ROC Curve:ROC曲線の下の面積)とは?
【参考】 ROC 曲線と AUC についてわかりやすく解説してみた
ROC曲線を見ることで、曲線の形状からも直感的にモデルの性能が読み取れます。
●ROC曲線が対角線に近い直線になる場合→モデルはデータをほとんど学習できておらず、性能は偶然と同程度
●ROC曲線が左上に大きく張り出す場合→モデルは非常に高い性能を持っていると考えられます
●ROC曲線が対角線よりも左上に位置する場合→モデルはランダムな予測よりも優れていると考えられます。AUCが0.7から0.9の範囲にある場合、モデルは実用的な性能を持っていると言えます。
●ROC曲線が特定の部分で急激に立ち上がる、または平坦になる場合→モデルが特定の状況下でのみ高い性能を発揮する、または特定の状況下で性能が著しく低下することを示唆しています。
③ 真陽性率[再現率] (Recall)
真陽性率 (Recall)は、実際に陽性であるもののうち、正しく陽性であると予測できた割合。再現率とも言います。
下図のピンクの部分の和、すなわち、検査で陽性かつ診断でも陽性(TP)を分子に、分母に診断で陽性だった人数を算出した比率を算出したものとなります。
④ 適合率(Prec.)
適合率(Precision/略してPrec.)は、陽性であると予測したもののうち、実際に陽性だった割合を表します。
下図のピンクの部分の和、すなわち、検査で陽性かつ診断でも陽性(TP)を分子に、分母に検査で陽性だった人数を算出した比率を算出したものとなります。
⑤ F1-score(F1)
F1-scoreは、 『compare_models』関数の出力では『F1』と表示されています。真陽性率 (Recall)と適合率(Precision/略してPrec.)の両方を加味した評価を表します。具体的には、適合率と真陽性率の調和平均がF1-scoreです。下記の式で算出されたものです。
F1 = 2 / (1/Precision + 1/Recall)
F1-scoreの求め方の詳細は、下図をご覧ください。
調和平均に関しては、速度の平均値を求める例がわかりやすい!下記のページを参照してみましょう。
カッパ係数は、ある現象を2人の観察者が観察した場合の結果がどの程度一致しているかを表す統計量で、0から1までの値をとり、値が大きいほど一致度が高いといえます。0.6以上であれば、観察者間の一致度(reproducibility)が十分高いと判断されます。求め方は、下図の左下の部分を参照してください。
マシューズ相関係数は、クラスの分布が不均衡なデータセット(一方のクラスが極端に少ないなど)において、モデルの性能を正確に評価するのに適しています。-1から+1までの値をとり、+1は完全な予測、0はランダムな予測、-1は完全な逆予測を表します。求め方は、下図の右下の部分を参照してください。
***********************************
さて、なぜこのような複数の評価指標を求めるのでしょうか?
極端な例を下図に示します。
ここでは、①のような混合行列で表されたデータとなった時に、②のように真陽性の患者がすべて偽陽性の患者になってしまったら、評価指標はどのように変化するかを示しています。
②は、検査で陽性の患者がすべて陰性と診断されてしまっていますから、明らかに、①と②は異なった状態と言えると思います。②の検査は、陰性を当てることはできるのですが、陽性を当てることはまったくできない検査ということが言えると思います。
それでも、①と②の正解率が同じです。しかし、真陽性率、適合率は異なってきます。
このように、極端な例をイメージすると、複数の評価指標を求めることが重要であることがわかると思います。











コメント
コメントを投稿